
Modifications of sediment deliver by rivers, climate change and human impact are modifying the dynamics of beaches leading to departures from equilibrium and consequent beach evolution. When erosion occurs, concerns may arise for its impact on societal use of beaches and safety of human settlements and infrastructures. In these cases, beach preservation strategies allow us to mitigate the above impacts.
Groins are a widely used structure that is used to protect beaches from erosion. We define groins as shore-perpendicular structures aimed at either (1) maintaining the beach behind them, or (2) controlling the amount of sand moving alongshore. An example of beach protection with groins is shown in Figure 1.

Figure 1. Beach recovery strategy at Cogoleto (Liguria region, Italy; from APAT, Atlante delle Opere di Sistemazione Costiera, Manuali e Linee Guida, 2007)
Groins can be classified as either "long" or "short," depending on how far across the surf zone they extend. Groins that traverse the entire surf zone are considered "long," whereas those that extend only part way across the surf zone are considered "short." These terms are relative since the width of the surf zone varies with the prevailing wave height and beach slope. During periods of low waves, a groin might function as a "long" groin, whereas during storms it might be "short." Groins can also be classified as either "high" or "low," depending on how high their crest is relative to prevailing beach berm levels. "High" groins have crest elevations above the normal high-tide level and above the limit of wave runup on the beach (USACE, 1992).
Being directed perpendicularly to the shoreline, groins may not be effective if cross-shore sediment transport is dominant, such as is typical in shallow beaches. In fact, groins function best on beaches with a predominant alongshore transport direction. They may also be inefficient if there is a large tidal range, allowing sand to bypass the structures at low tide or to overpass at high tide. Bypass of groins by sediments is defined as the movement of sediments along shore beyond the groins in the seaward direction. Overpassing is the movement of sediments above the groins when these are submerged.
Groins may be effective where sand movement alongshore is to be managed, such as where there is a divergent nodal region in alongshore transport, for instance where the curvature of the coast changes, where intruding sand is to be managed, such as in correspondence of the banks of inlets, at the down-drift side of a large harbor breakwater, and other situations where alongshore sediment transport is a reason of concern.
Groins may or may not be permeable to sediments. Impermeable groins are constructed of various materials, typically by boulders, and are designed to completely interrupt any available littoral drift in the proximity of the undisturbed shoreline. Thus, the littoral drift is forced around the seaward end of the groin or, if sufficient beach material has been trapped by the groin, to pass over its top. Permeable groins are designed so that an appreciable quantity of the available littoral drift will pass directly through its structural components. They are frequently built with wood elements.
Groin functional design has been discussed by several authors, including Bruun (1952, 1972), Balsillie and Berg (1972), Balsillie and Bruno (1972), Nayak (1976), Fleming (1990), and the U.S. Army Corps of Engineers (USACE, 1992). They offer the basis for empirical design based on laboratory experiments and field observations. The former may suffer from distorsion in small scale physical models while the latter suffer from specificity of beach conditions, wave forcing and sediment dynamics in general. A comprehensive discussion has been provided by Kraus et al. (1995).
Wave behaviours are leading parameters as they determine alongshore sediment transport. Therefore, a rigorous statistical analysis of wave forcing, and in particular wave height and variability, is needed. Groin length is a leading parameter as well, and in particular the sea depth at the tip of the groin. Furthermore, another leading parameter for groin fields is the groin length to spacing ratio.
Practical experience reveals that modification of the shoreline accretion induced by groins rarely brings the shoreline itself to reaching the seaward end of groins. Typically, the updrift shoreline reaches only a modest distance to the groin tip. Such a behaviour indicates that sand bypassing and permeability of the groin to sand, as well as variability in wave forcing, play an important role in determining transport around the groin and resultant local and regional shoreline change. About the time of development of the new beach configuration, Nersesian et al. (1992) found that groin compartments were still slowly filling in the predominant direction of the shoreline sediment transport after almost three decades after displacement. Such functioning can be explained by the process of bypassing, whereby each compartment deprives sand to neighboring downdrift compartments during shoreline evolution.
Permeability is a desired feature of groins, in order to avoid accumulation of large volume of sand against them, which can be transported offshore during dominant cross-shore sediment transport. For the same reason, groins should not extend too far offshore beyond the average wave breaker line.
The evolution of the shoreline profile after the displacement of groins can be represented trough the progress in time of a suitable spatial coordinate x(t) which can be expressed through an analytical relationship. The variables that are important in groin design can be determined through dimensional analysis. In engineering and science, dimensional analysis allows one to inspect the relationships between different physical quantities by identifying their fundamental dimensions and units of measure and tracking these dimensions as calculations or comparisons are performed. We are not inspecting the details of dimensional analysis here. Dimensional analysis for groin functioning indicate that several parameters may be effective to determine the shoreline evolution. The engineer can design some of them, like groin spacing, length and permeability, which is in turn determined by groin elevation and porosity. Other parameters related to wave forcing can be controlled by displacing other protection structures like breakwaters.
Kraus et al. (1994) provide a comprehensive overview of parameters governing the effect of groins. Parameters related to groin structure are:
- Length;
- Spacing between groins;
- Elevation;
- Porosity;
- Tapering;
- Angle to the shoreline;
- Shape (as straight, angled, T-head, spurred etc.).
Parameters related to beach and sediment are:
- Depth at tip of groin;
- Beach morphology (slope, berm height, shape of the shoreline etc.);
- Depth at the average breaker line or beach closure;
- Sediment availability;
- Grains size and variability;
- Sediment density.
Parameters related to waves, wind and tide are:
- Wave height and variability;
- Wave period and variability;
- Wave direction and variability;
- Wind speed and variability;
- Wind direction and variability;
- Wind duration and variability;
- Tidal range.
Furthermore, functioning of groins may be affected by wave diffraction if it occurs. The impact of diffraction may be difficult to predict.
Design of groins can be carried out by applying empirical relationships derived from laboratory experiments and analysis of observations. The use of rules of thumb and empirical formulations is widely diffused as it is difficult to provide a physically-based interpretation of processes that are affected by large uncertainty. However, after a preliminary shape has been determined for groins it is suggested to carry out a numerical simulation of the beach evolution, which can provide support to the design and subsequent monitoring activities.
Preliminary design is often carried out by following the so-called “λ shoreline” rule of thumb, originally termed the “one-third rule” (Bodge 1998). The rule says that the post-project coastline during mean low water level is located between about λ=1/3 and λ=2/3 of the distance between adjacent groins measured behind the structures' seaward face (see Figure 2). Larger λ values, that may even exceed 2/3, may be appropriate for energetic environments, larger distances between groins, uncertainty in long term sediment supply and the whole design process. In general, larger λ values imply a more prudent design (Bodge, 2003). These values for λ are confirmed by several field observations that are summarized by Bodge (2003). The denomination “one-third rule” is explained by the above indicated minimum λ=1/3 value. The rule is considered applicable where the angle between the wave crest and the line connecting the tips of the structures (control line) is small, that is, lower than 25°-30° (that is, wave crest is nearly parallel to the control line).
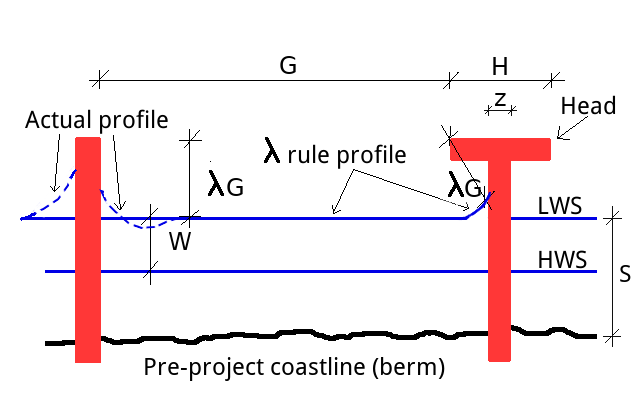
Figure 2. λ rule for the preliminary design of groins. LWS and HWS indicate low and high water shoreline, respectively.
Actually, the λ shoreline rule would predict a rectilinear line shape for the equilibrium profile of the beach when straight (non T-shaped) groins are displaced orthogonally to the shoreline. However, settlement of sediments tends to originate a curved shape of the after-project shoreline along the sides of the groin, for the effect of diffraction and sediment interception by groins. Empirical rules have been proposed to determine the actual equilibrium profile of the beach, which are not discussed here.
Another example of application of the lambda rule is shown in Figure 3, with irregularly shaped groins.
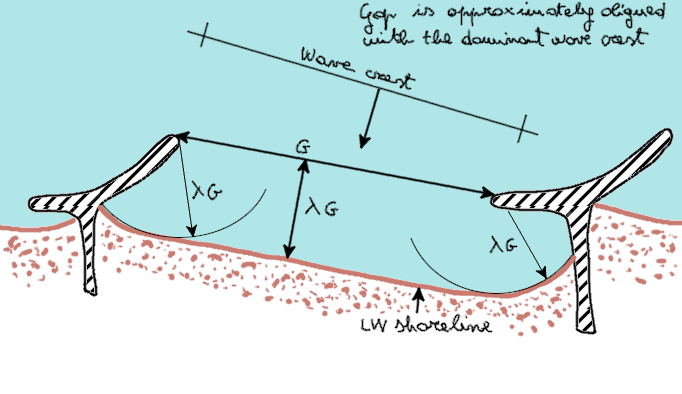
Figure 3. λ rule for the preliminary design of groins with an irregular shape. Redrawn from Bodge (2003).
We adopt here the following steps for groin design as summarized by Bodge (2003).
- Step 1: estimation of the wave statistics, in particular the wave angle, and longshore sediment transport potential, at selected locations of interest. If an extended data set is not available, useful indications can be derived by looking at the beach morphology and/or displacement of sand in different seasons against existing structures or irregularities in the beach profile.
- Step 2: identification of the extension of the intervention, by taking into account the dynamics of longshore sediment transport. Structures should be placed in correspondence of relevant transport and should end where the sediment transport gradient is low.
- Step 3: identification of the design location of the post-project berm.
- Step 4: estimation of the probable post-project slope of the beach, by looking at adjacent beaches. We should take into account that the post-project beach is expected to be slightly gentler sloped than the non-stabilized beach, because of the decreased (diffracted) wave energy that reaches the beach.
- Step 5: prediction of the horizontal distance W between the mean low water and mean high water shorelines. We should also predict the horizontal distance S between the mean low water shoreline and the berm.
- Step 6: identification of the number of beach cells, n, and average gap width, G, and groin head width, H. For T shaped groins H > z, where z is the width of the groin main body. Therefore, the total shorefront length of the intervention, L, which is composed of n beach cells, is expected to L=n(G+H).
- Step 7: design of the length and head-width of groines, H (see Figure 2).
- Depending on the design position of the low water shoreline, length and shape of the groin, as well as head-width, are determined by applying the λ rule. A T shaped groin allows one to reduce the groin length, as the T implies that the low water shoreline is shifted seaward according to the λ rule itself. If one wants to bring the low water shoreline up to the groin head, then a T shape should be adopted, and then λ rule implies that H=2λG + z (see Figure 2). In some cases it may be required that the mean high water shoreline reaches the head. Namely, H= 2(λG+W) + z. In general, then, H=2(λG+X) + z
where 0≤X≤W. Therefore one obtains
L = n(G+2λG+2X+z),
L = nG+2nλG+2nX+nz,
2nλG+nG=L-2nX-nz,
G(2nλ+n)=L-2nX-nz,
G=(L/n–2X-z)/(2λ+1).
If the gap width reduces too much, then a rectilinear groin may be adopted and its length increased in order to reach the desired position of the shoreline.
In practice, we select a number of beach cells, n, for a identified value of λ and desired value of X in order to develop a physically reasonable gap width, G. G values less than about 20 m are not generally recommended, at least for recreational beaches. In fact, small openings have limited aesthetic; moreover, strong rip currents may be originated with small openings. On the other hand, gap widths greater than about 100 m are not recommended as well, because distant structures may be not effective in determining an extended reshaping of the beach.
Additionally, for recreational beaches, it is advisable that the head widths are smaller than the gap widths (H≤G). - Step 8: positioning of the gaps and heads along a line that is S+λG seaward of the target (design) berm location, where S is the distance from the new low water profile and the berm.
- Step 9: orientation of the gaps to make them more closely parallel with the average, or principal, crest orientation of the breaking waves at each cell. The aim is to minimize the wave crest angle with the orientation of gaps. If the terminal structure in a field employs a head or spur on its downdrift side, it is better to offset it seaward than landward. While intuition suggests that a landward offset would offer a more natural transition from the structure to the downdrift shoreline, the λ rule suggests that it inherently induces a crenulate bay that will erode into the native beach.
- Step 10: prediction of the impact of extreme waves. Once satisfied that the project lay-out's predicted shoreline and berm will satisfy the "target" shoreline for the principal wave direction, then the shorelines and berm locations are predicted for extreme wave directions. This aims to assess the degree to which the structures might be exposed to seasonal or storm events where the waves deviate from their average direction. Adjustments may be necessary to accommodate the wave extremes.
- Step 11: the landward head of the groins are extended to reach the berm and buried within the beach fill.
- Step 12: The elevation of the landward heads should be determined to minimize wave overtopping during the design event of interest, which typically includes typical seas at higher high tides. The elevation of the stems may be lower than the heads, but of sufficient elevation to prevent tidal overtopping at higher high tides. The profile elevations of the terminal structures should be higher than the design beach profile predicted adjacent to the structure. In the case of a rock structure, the crest elevation should be not less than 1⁄2 armor stone diameter above the predicted design profile (plus some contingency).
Groin fields should be built from the downdrift to updrift direction. A desired evolution of groin field is that they are filled.
Main parameters for groin design are given in Figure 4.
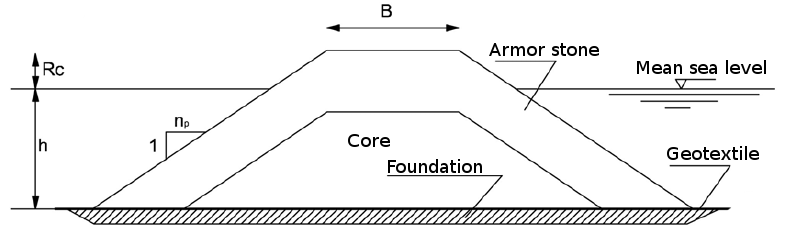
Figure 4. Structure of a groin.
Orders of magnitude for the principal parameters of groins are as follows.
- h - depth of the basement of the groin head with respect to mean sea level (msl)- From 2.5 to 4 m.
- Rc - height of the groin top with respect to mean sea level - From 0.5 to 1.5 m.
- Depth of the of the groin basement landward with respect to mean sea level - From 1.0 to 2.0 m.
- B - Width of the groin top - From 3.0 to 6.0 m.
- 1/np - Slope of the groin sides - From 1:1 to 1:2.
- Thickness of foundation - From 0.5 to 1.0 m.
Stability of groins should be verified against extreme sea conditions. If groins are made by boulders, the stability of the single stone should be checked against the expected wave energy.
The preliminary design of groins based on empirical rules should be verified through numerical modeling of beach evolution. Models are based on subdividing the shoreline in adjacent cells for which sediment transport rate is estimated by applying suitable relationship, like for instance the CERC formula. Limiting configurations of the beach, for instance due to emerging rock layers, are subsequently identified, as well as sources and sinks of sediments.
Once the model is set up, groins are displaced along the shoreline and modified sediment transport rates are computed. To this end, one need to estimate the volume of sediments that is intercepted by groins and the volume of sediments that bypass or overtop the structure.
Numerical models were proposed by the literature to estimate beach evolution after the displacement of groins. We summarise here below the theory of the GENESIS model (GENEralized model for SImulating Shoreline change; Hanson, 1988; Kraus et al., 1995). GENESIS simulates shoreline change as caused primarily by wave action. The model is based on the one-line concept, which assumes that the beach profile remains unchanged, thereby allowing beach change to be described uniquely in terms of the shoreline position. In fact, it is frequently observed that the beach profile maintains an average shape that is characteristic of that particular coast. Beach features like slope and singularities are preserved in the long term. Although seasonal changes in wave climate cause the position of the shoreline to move in a cyclical manner, the departure from the characteristic shape are relatively small. Therefore the beach profile responds to wave action by moving back and forth during erosion and accretion, under the assumption that the profile moves parallel to itself. If the profile shape does not change, any point on it is sufficient to specify the location of the entire profile with respect to a baseline. Groins may act as fixed points along the shoreline therefore inducing a seaward shift of the shoreline.
Important implications of the above assumption of steady profile are that only longshore sand transport can be taken into account and that the profile is always in equilibrium. However, cross-shore transport can be simulated within GENESIS in a schematic way, in terms of non-wave induced sources and/or sinks of sands along the coast.
The second major assumption of the model is that sand actively moves over the profile to a certain limiting depth, beyond which the bottom does not move. This depth is called the depth of closure Dc. GENESIS uses a simple relation for calculating the depth of closure according to the relationship
Dc=2 Hmax
where Hmax is the maximum annual wave height. Evolution of beach occurs according the scheme presented in Figure 5.
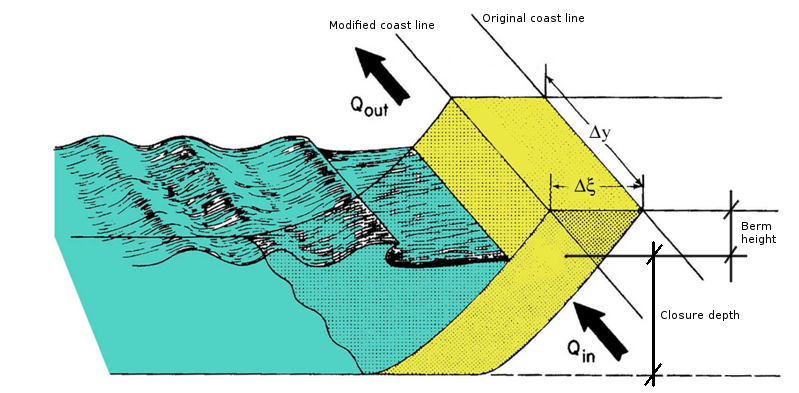
Figure 5. Computation of beach profile under the effect of longshore sediment transport according to the one-line model. Source: tutorial of prof. Musumeci, University of Catania
The model is based on the application of mass conservation in each beach cell. For applications involving bypassing of sand at structures, knowledge of the depth to which sand is actively transported alongshore is required. This depth, assumed to be related to the incident wave conditions which vary with time, is called the depth of longshore transport. The latter parameter affect the rate of sand that is transported by waves around groins. A through analysis of groins bypassing should include the cross-shore distribution of the longshore sand transport rate, as well as the two-dimensional horizontal pattern of sand transport. In view of the uncertainties related to evaluating these processes, a simple assumption producing reasonable results was adopted.
The fraction F of sand that is transported over a groin and through it is represented by a permeability factor P, and the amount passing around the seaward end is represented by a bypassing factor B (Hanson & Kraus 1989), such that
F=P(1-B)+B
where 0≤P≤1, and 0≤B≤1. P is estimated depending on the shape of groins and in particular the presence of apertures in their cross shore direction. P values are suggested by the literature for typical groin shapes. Groins made by boulders have a P value that is close to zero. The actual volumetric sediment transport rate at the groin Q'G is related to the calculated potential rate at the groin QG as
Q'G=F QG.
The permeability factor is assigned based on groin elevation, groin porosity, and tide range, and the bypassing factor B is calculated in the model at each time step through the relationship
B=1-DG/DLT
where DG is the sea depth at the groin seaward end at a particular time step, and DLT is the depth of active longshore sediment transport, which can be assumed to be about 1.6 times the significant breaking wave height (Hanson & Kraus 1989). Therefore groin bypassing is dictated by sea depth at the groin seaward end and wave behaviors.
Empirical formulation are used within GENESIS to estimate bypassing for angled groins, shape of the sea bottom profile, impact of refraction and diffraction. We are not interested in the details herein. Once the after-project sediment transport rate is estimated, beach profile can be determined. The λ rule and other empirical rules of beach evolution can provide a benchmark to verify the reliability of the simulation. A user interface is available in GENESIS to allow implementation to a diverse variety involving arbitrary configuration and combinations of groins.
The stabilization of beach fill by structures may be warranted at sites where erosion stress is sufficiently severe to require otherwise impractical (frequent) renourishment intervals; or where the proximity of natural resources or marine structures preclude construction of a wide beach fill; or where the project shoreline is advanced far seaward of the adjacent shoreline. Adverse impacts to downdrift shorelines may be minimized by (i) advance-nourishment of the structures’ impoundment field with imported beach fill, (ii) use of T-head or other headland structures that do not promote rip currents and offshore losses, and (iii) termination of the structural field in non-accelerating longshore transport potential.
Particular care should be given to the preliminary interpretation of the processes leading to shoreline shape. Observation is the basis for a successful design.
Balsillie, J.H. and Berg, D.W. 1972. State of Groin Design and Effectiveness. Proc. 13th Coastal Eng. Conf., ASCE, 1367-1383.
Balsillie, J.H. and Bruno, R.O. 1972. Groins: An Annotated Bibliography. Miscell. Paper No. 1-72, Coastal Eng. Res. Center, Vicksburg, Miss.
Bodge, K. R., 2003. Design Aspects of Groins and Jetties. In: Advances in coastal structure design. Ed. R. Mohan, O. Magoon, M. Pirrello. American Society of Civil Engineers (ASCE). Reston, VA. ISBN 0-7844-0689-8. Pp. 181-199
Bruun, P. 1952. Measures Against Erosion at Groins And Jetties. Proc, 3rd Coastal Eng. Conf., ASCE, 137-164.
Bruun, P. 1972. The History and Philosophy of Coastal Protection. Proc. 13th Coastal Eng, Conf., ASCE, 33-74.
Fleming, C.A. 1990. Principles and Effectiveness of Groynes. Coastal Protection, Pilarczyk, K.W., (Ed.), Balkema Press, Rotterdam, 121-156.
Hanson H., 1988. GENESIS-A generalized shoreline change numerical model. Journal of Coastal Research, 5(1), 1-27, Charlottesville (Virginia). ISSN 0749-0208.
Hanson, H. and Kraus, N. 2001. Chronic Beach Erosion Adjacent to Inlets and Remediation by Composite (T-Head) Groins. U. S. Army Corps of Engineers, Waterways Experiment Station, Vicksburg, MS, ERDC/CHL Coastal Engineering Technical Note CHETN-IV-36, 15 pp, June 2001.
Kraus, N. C., Hanson, H., & Blomgren, S. H. (1995). Modern functional design of groin systems. In Coastal Engineering 1994 (pp. 1327-1342).
Nayak, U.B. 1976. On the Functional Design and Effectiveness of Groins in Coastal Protection. Ph.D. Dissertation, U. of Hawaii, 205 pp. USACE, (1992). Coastal Groins and Nearshore Breakwaters. In: Engineer Manual, (1992).
Download the powerpoint presentation of this lecture
Last updated on March 29, 2023
- 1467 views
