Adapting to climate change requires a through assessment of how climate is changing and how such change impacts the local socio-economic and environmental context. The interaction between climate and society depends on how the climatic forcing affects the environmental features that are relevant to societal organisation and security. To provide a simple example, the impact of a meteorological drought depends on how lack of rainfall is reflected into lack of surface water and groundwater, and how local municipalities cope with limited water supply. If the local water supply system is resilient - for instance because it relies on large reservoirs - the impact of droughts can be mitigated with a proper management,

Assessing the impact of climate is instrumental to estimate the probability that a given critical event may occur, which in turn it is an essential information to assess the risk for the local communities associated to such event. Risk estimation is essential to identify mitigation and adaptations actions and their priority.

Communities may be exposed to several risks related to climate. According to the United Nations Office for Disaster Risk Reduction (UNDRR), the multi-hazard concept refers to “(1) the selection of multiple major hazards that the country faces, and (2) the specific contexts where hazardous events may occur simultaneously, cascadingly or cumulatively over time, and taking into account the potential interrelated effects.”

These definitions of multi-hazard represent two major categories in which multi-hazard approaches can be classified: (i) independent multi-hazards approaches, where single hazards are just overlayed and treated as independent phenomena, and (ii) approaches that consider multiple hazards and their potential interactions. In what follows, in order to refer to a simplified context, we concentrate on the treatment of independent phenomena, whose risk is estimated one by one. Risk estimation is essential to identify the prioritary threats.

For a given threat, several solutions may be available for adaptation. Again, estimating the priority of each solution is an important step to elaborate a consistent adaptation plan.

But what is risk, and can we estimate it?

When dealing with natural hazards, risk is usually estimated on the following premises:

• The risk R induced by a considered event is given by the combination of hazard P, exposure E and vulnerability V.
• R is a measure of the expected damage during an assigned time period given by a considered event, depending on the vulnerability of the considered system and the potential damage if the event actually occurs, which is in turn related to the nature and quantity of the exposed goods.
• The hazard P is given by the probability of the considered event to happen in a specific context e the assigned time period. For instance, it can be the probability of an inundation occurring in a year.
• Vulnerability V is the probability that the system (for instance a given societal asset) is damaged at a certain level, if the considered event occurs. For instance, if a town is protected against floods by levees then the probability of being damaged by a flood is lower than in the absence of any protection.
• The exposure E reflects the presence of goods exposed to the considered event. For instance, it can be associated to the economic value of the damage induced by an inundation.

Under the above premises, risk \(R\) can be estimated through the relationship

$$R = P V E. (1)$$

According to (1), risk is then expressed in monetary terms. On the one hand this solution is practical; on the other hand, it may be difficult to associate a economic value to intangible assets. Furthermore, it may be inappropriate to estimate the physical risk for human beings as for economic damage. Therefore, some authors suggest that the physical risk for humans is estimated separately, by using proper procedures for evaluating probability, vulnerability and exposure. In what follows we refer for simplicity to a situation where physical damage for humans is excluded.

While eq. (1) looks extremely simple, actually the estimation of \(P\), \(V\) and \(E\) is not straightforward. Let us start with the estimation of \(E\), which is relatively easier.

Exposure estimation

\(E\) is given by the value of the goods that are damaged/destroyed if the event occurs, which can be estimated once the magnitude of the event and its consequences have been assessed, by introducing proper assumptions.

The critical phases for estimating \(E\) are, in fact, the definition of the magnitude and impact of the event and the definition of the economic value for some goods, that may be not easily determined. For instance, what is the economic value of a cultural heritage, like a famous painting? What is the economic value of an environmental disaster, which may cause an irreversible environmental deterioration? We will not discuss in detail here how to deal with intangible damage, but it is important to be aware of its critical role.

In general, estimating \(E\) requires an interdisciplinary effort. One has to first make the inventory of the exposed goods, which depends on the intensity of the event. Then, an economic evaluation is needed.

Vulnerability estimation

Estimation of \(V\) is in most of the cases an essentially technical step. It requires a careful consideration of the protection measures against the considered event. \(V\) is usually assumed to vary in the range [0,1]. If the local communities are fully protected, then \(V=0\). If there is no protection at all, \(V=1\).

Vulnerability also depends on the intensity of the event. An intervention to increase vulnerability is generally effective against a limited range of event intensities only. For instance, think of a water reservoir that is built to cope with droughts. The volume stored in the reservoir is limited, of course. Thus, it can protect the downstream community only for a limited duration of the drought. If such duration is exceeded, then the vulnerability is reset to 1. The damage that is caused when the above limit is exceeded may be even more impactful with respect to absence of any protection. In fact, the presence of the reservoir may induce the communities to rely on water supply with more confidence therefore weakening their resilience.

In turn, vulnerability has an impact on exposure. In fact, a reduced vulnerability may stimulate the investment by the communities on their goods thereby increasing their value and thus exposure.

Probability estimation

Probability describes the likelihood of the event in the considered context. Probability is quantified as a number between 0 and 1 (where 0 indicates impossibility and 1 indicates certainty). The higher the probability of an event, the higher the likelihood that the event will occur. Procedures for describing and estimating probability are the subject of probability theory. It is a fascinating field that has a long history, ad relies on a systematic organisation of axioms, assumptions, theorems and methods.

Actually, probability describes in formal terms a knowledge that is part of our everyday experience. Despite the mathematical development looking complicated, the results and conclusions are often intuitive. Basing on the latter consideration, we will introduce probability through simple technical examples, for the purpose of immediately understanding how probability can allow us to quickly and easily reach our target, that is, a numerical estimation of the likelihood of an event. It is important to point out that what follows is not a formal introduction to probability. We are taking a simplified route: there is much more to say and learn to become a probability expert. We will make an effort to suggest readings for those that are interested in gaining a full comprehension of this fascinating theory.

3. An informal introduction to probability

To informally introduce probability we refer to a casual event (or random event): it is an event that it is not predictable with a deterministic approach. All natural hazards are associated to the likelihood of random events.

Typical examples of random events (not related to natural hazards) are tossing a coin and rolling a dice. The first step to analyse a random event is to identify all possible outcomes, which build up the sample space. For coin tossing, if we exclude the outcome given by the coin landing on the edge, the sample space is formed by two outcomes, head or tail, that are mutually exclusive, that is, they cannot happen at the same time.

By taking into account that probability is expressed by a number in the range [0,1], as we anticipated above, where 0 means impossibility and 1 means certainty, try to answer this question: what is the probability of getting a head from a coin tossing? We may answer by adopting two approaches:

• We may elaborate a reasoning to conclude that the same amount of probability (the same probability mass) must be shared by the two outcomes. Therefore we conclude that the probability of getting a head \(H\) should be in the middle between impossibility and certainty, and therefore we may conclude that \(P(H)=0.5\).
• On the other hand, we may decide to move forward by making an experiment and toss the coin several times. If, for instance, we toss the coin 100 times and get 46 heads and 54 tails, we may conclude that we have more or less the same probability of getting either of the two possible results. We may also realise that a wise way of translating the outcome in numerical terms may be to compute probability with the relationship \(P(H)=46/50\approx 0.5\).

Both of the above approaches are correct. The first one may be subjective, but has the advantage of not requiring an experiment, which is useful if the random event cannot be repeated several times. The first one is a kind of what is called Bayesian estimation of prior probability (where prior means antecedent to any further collection of evidence). The second approach applied the frequentist estimation of probability, through which the probability mass of a given outcome is estimated by performing several experiments and then computing:

$$P\left(H\right)=\frac{N_H}{N_{tot}} (2)$$

where \(N_{tot}\) is the total number of experiments and \(N_H\) is the number of outcome \(H\) after the experiment. Of course, we understand that \(N_{tot}\) must be large to make the above estimation reliable. With a few number of tossings uncertainty would remain large.

The above consideration suggest how probability can be estimated. However, to move forward with our understanding we need to formally define what probability is. We may define it through the Kolmogorov axioms:

• Axiom 1: The probability of an event is a real number greater than or equal to 0.
• Axiom 2: The probability that at least one of all the possible outcomes of a process (such as tossing a coin) will occur is 1.
• Axiom 3: If two events A and B are mutually exclusive, then the probability of either A or B occurring is the probability of A occurring plus the probability of B occurring.

The first two axioms reflect our assumption above that probability lies in the range [0,1]. The third axioms implies that the \(P(H)+P(T)=1\), where \(P(T)\) is the probability of getting a tail, which is consistent with our assignment \(P(H)=P(T)=0.5\).

Thus, we may conclude that there are two definitions of probability. The frequentist definition is a standard interpretation of probability; it defines an event's probability as the limit of its relative frequency in a large number of trials. Such definition automatically satisfies Kolmogorov's axioms. The Bayesian definition associates probability to a quantity that represents a state of knowledge, or a state of belief. Such definition may also satisfy Kolmogorov's axioms, although it is not a necessary condition.

Frequentist and Bayesian probabilities should not be seen as competing alternatives. In fact, the frequentist approach is useful when repeated experiment can be performed (like tossing a coin), while the Bayesian method is particularly advantageous when only a limited number of experiments, or no experiments at all, can be carried out. The Bayesian approach is particularly useful when a prior information is available, for instance by means of physical knowledge.

By extending the knowledge gained so far to the experiment of rolling a dice, we may easily conclude - through Bayesian reasoning or through experiments - that the probability \(P(i), i=1,...,6\ = 1/6\), namely, probability mass is equally distributed over the possible outcomes.

Note: in this case we associated an event - the dice showing one specific face - to a number: thus, we implicitly associated a random variable to an outcome from an event. A random variable is a mathematical formalization of a quantity or object which depends on random events.

For the event of rolling a dice, however, an interesting question may arise. What is the probability of getting an outcome lower or equal to, say, 4? A simple reasoning brings as to write:

$$P\left(i\leq4\right)=P\left(1\right)+P\left(2\right)+P\left(3\right)+P\left(4\right)=\frac{4}{6}=\frac{2}{3} (3),$$

thus obtaining an estimate of what is called cumulative probability. This is an interesting development as we may be interested, for instance, in the probability that the water level into a river does not exceed the level of the levees.

Important: eq. (3) applies the addition rule for probability, for the case of mutually exclusive events.

Another example is the computation of the probability of the sum of two dice rollings. It is explained in Figure 1, which also indicate the probability mass of each possible outcome.

Figure 1. Outcomes from the sum of two dice rollings, with the probability mass of each possible outcome. By Niyumard, CC BY-SA 4.0, via Wikimedia Commons.

An example of computation of probabilities for the experiment of rolling a dice may be helpful to introduce the following steps. We develop with experiment with the R software.

Exercise: computation of probabilities with the R software

The outcome from simulating a dice rolling can be easily generated with the R software with the instruction below, which you may copy and paste in the R console:

floor(runif(1,1,6.9999))

which generates a single random number in the range [1,6.9999] by sampling from a uniform distribution. The function floor then rounds it to the lowest integer. With the following instruction we can generate the results from one million rollings and put them in a vector names "rollings":

rollings=floor(runif(1000000,1,6.9999))

It is now straightforward to compute the probability of the outcome - say - 1 by adopting the frequentist approach:

length(rollings[rollings==1])/1000000

which will result very close to 1/6. The same computation can be done for the other outcomes, which will yield the same result. We can now compute the cumulative probability of getting an outcome lower or equal to 4:

:

length(rollings[rollings<=4])/1000000

which is very close to 2/3.

Continuous random variables

The outcome from rolling a dice is an integer random variable. For several natural hazards, the random variable is a real number. Think, for example, to maximum annual daily rainfall. For real random variable, we will never get, from an experiment, an outcome that is precisely coincident to an assigned real number, which has infinite digits. Therefore the probability of getting such assigned value tends to zero. How can we compute the probability of a given outcome then?

An empirical solution for computing the probability of getting an outcome \(x\) from the random variable \(X\), namely, \(x=X\) may be to split the domain of \(X\) into segments with finite length, and then compute the frequency the outcome \(x\) falls into the interval \(\left[x-\Delta x, x+\Delta x\right)\). However, if one adopted this approach then probability would depend on the choice of \(\Delta x\), which would not correct.

To make the estimate of probability independent of \(\Delta x\) we need to define the probability density \(p(x)\), namely, the probability per unit length, which can be computed with the relationship:

$$p\left(x\right)=\lim\limits_{\Delta x \to 0}\frac{F_r\left(x-\Delta x;x+\Delta x\right)}{2\Delta x}$$

where \(F_r\left(x-\Delta x;x+\Delta x\right)\) is the frequency of \(x\) falling in the above interval, namely: $$F_r\left(x-\Delta x;x+\Delta x\right)=\frac{N\left(x\right)}{N}$$ where \(N \rightarrow \infty\) is the number of experiments.

Note that probability density is expressed in units of 1/[\(x\)] where [\(x\)] is the unit of \(x\).

Exercise: computation of probability density with the R software

One million of outcomes from a uniform random variable in the range [1,10] can be easily generated with the R software with the instruction below, which you may copy and paste in the R console:

pd1=runif(1000000,0,10)

Then, the probability density of the random variable falling into the interval [0,0.1] can be computed as

length(pd1[pd1>=0 & pd1<=0.1])/1000000

With a cycle, we can compute the probability density over the full range of \(x\) and put the results in the vector pd2:

pd2=0

      for (i in 1:100) 
      {pd2[i]=length(pd1[pd1>=(0+(i-1)*0.1) & pd1<=(i*0.1)])/1000000/0.1}

and then we can plot the resulting probability density with the instruction:

plot(pd2,type="l")

which show that the density is approximately uniform. It is also interesting to plot the cumulative probability, with the instruction

plot(cumsum(pd2*0.1),type="l")

which, as expected, is a straight line summing up to 1.

Actually, what we plotted with the last instruction is the integral of the probability density, namely, the cumulative probabiity:

$$P\left(X\leq x*\right)=\int_{x=0}^{x=x*}p\left(x\right)dx.$$

Indeed, for continuous random variables the cumulative probability is the integral of the probability density.

Probability distributions

A probability distribution (or probability function) is an analytical function that assigns a probability to a considered random event. To define a probability distribution, one needs to distinguish between discrete and continuous random variables. We will focus on the continuous case.

If an analytical function exists for p(x), this is the probability density function, which is also called probability distribution function, and is indicated with the symbol "pdf". If the probability density is integrated over the domain of X, from its lower extreme up to the considered value x, one obtains the probability that the random value is not higher than x, namely, the probability of not exceedance or cumulative probability, which is often indicated with the symbol "CDF".

Example: the Gaussian or normal distribution The Gaussian or Normal distribution, although not much used for the direct modeling of hydrological variables, is a very interesting example of probability distribution. I am quoting from Wikipedia:

In probability theory, the normal (or Gaussian) distribution is a very common continuous probability distribution. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known [...]

The normal distribution is useful because of the central limit theorem. In its most general form, under some conditions (which include finite variance), it states that averages of random variables independently drawn from independent distributions converge in distribution to the normal, that is, become normally distributed when the number of random variables is sufficiently large. Physical quantities that are expected to be the sum of many independent processes (such as measurement errors) often have distributions that are nearly normal. Moreover, many results and methods (such as propagation of uncertainty and least squares parameter fitting) can be derived analytically in explicit form when the relevant variables are normally distributed."

The probability density function of the Gaussian Distribution reads as:

$$p \left( x\vert \mu ,\sigma \right) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{\left(x-\mu\right)^2}{2\sigma^2}},$$

where \(\mu\) is the mean of the distribution and \(\sigma\) is its standard deviation.

 
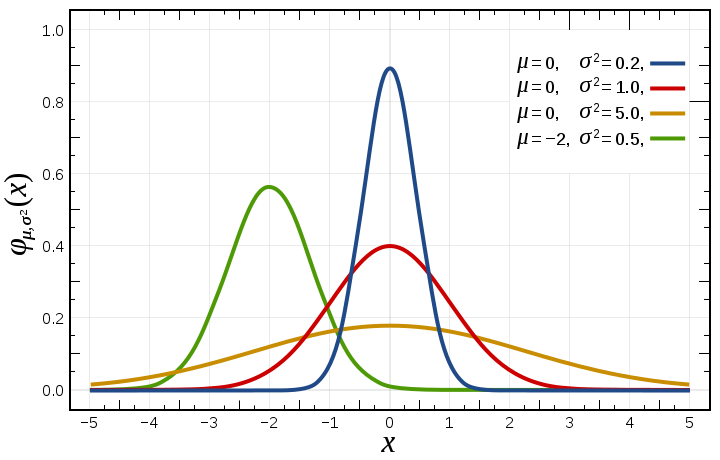
Figure 2. Probability density function for the normal distribution (from Wikipedia)

4. Relationship between P, V, E and R

It is interesting to analyze the relationship between P, V, E and R. Such relationship can be studied by by analisying the progress of E, V and R as a function of P. An example of such progress, which of course depends on the considered systems and the type of risk, is presented in Figure 3. Some interesting features can be highlighted.

 
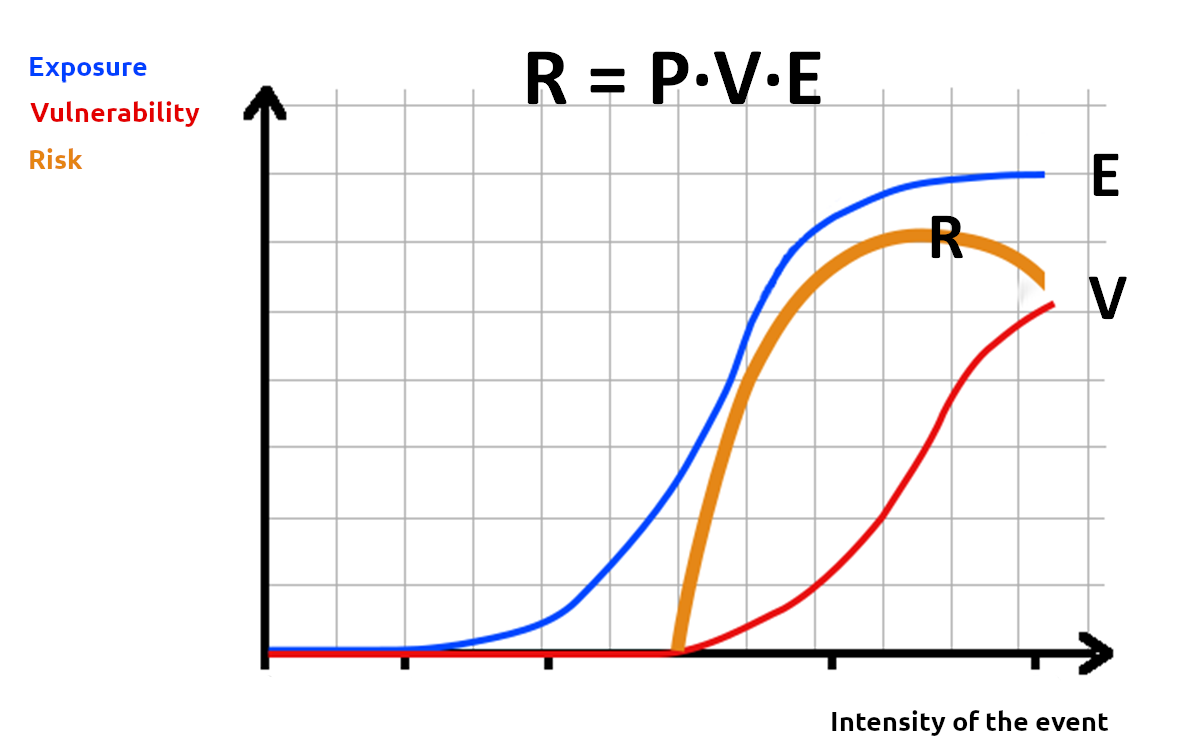
Figura 3. Example hazard-exposure-vulnerability curve (PEVR curve).

First of all it should be noted that in Figure 3 the hazard is expressed in terms of intensity of the event, to make the figure more illustrative. For each event, the intensity is univocally associated to its hazard. The higher the intensity, the lower the hazard. It should be noted that such association between intensity and hazard may vary after climate change.

As the intensity increases, vulnerability and exposure typically increase. For low intensity exposure and vulnerability may be negligible or null, but with increasing intensity they generally increase as well. As intensity attains very high values both vulnerability and exposure tend to asymptotically reach a maximum.

The risk R, which results from the product of hazard, vulnerability and exposure, has a different trend because as the intensity increases hazard decreases. In general it is possible to identify a critical intensity which corresponds to the maximum risk.

Climate change results in the change of the hazard associated to events of a given intensity. Therefore, for a given hazard we experience a change in vulnerability. The task of adaptation actions is to reduce vulnerability and/or exposure, in order to compensate for the increased hazard.

The above procedure highlights and vulnerability, exposure and hazard estimation are critical for the design of a successful climate action. While vulnerability and exposure are relatively easy to estimate, hazard estimation is challenging, not to mention the additional uncertainty induced by climate change. Climate predictions are of course an essential information to estimate future hazard. These considerations, moreover, highlight the essential value of uncertainty estimation for future climate scenarios, as the future hazard strictly depends on climate prediction uncertainty.

Last updated on March 2, 2023