Stima di portata ed idrogramma di piena

Le alluvioni sono causa di numerosi disastri naturali che accadono con sempre maggiore frequenza sul territorio italiano ed Europeo (si veda, ad esempio qui e qui). Durante le alluvioni la corrente fluviale è dotata di elevata energia e costituisce quindi un rilevante pericolo per le infrastrutture e le aree urbanizzate: ad esempio, a questo link è possibile osservare un breve filmato ripreso alla Chiusa di Casalecchio durante la piena del Fiume Reno (Bologna) del 2013. A questo link è invece possibile vedere il video di una piena che si è verificata nel 2015 sul Fiume Nure a Piacenza. Questo video mostra invece un'alluvione che si è verificata in California nel 2018.

La stima della piena e dell'idrogramma di progetto rappresenta un compito impegnativo che viene frequentemente posto al progettista, necessario per la progettazione di numerose infrastrutture quali ad esempio ponti, protezioni fluviali, opere di presa, briglie e argini. In taluni casi pratici è necessaria la conoscenza dell'intero idrogramma di piena, mentre in altri casi è sufficiente la conoscenza della sola portata al colmo.

L'idrogramma è composto di diverse parti distinte la cui nomenclatura è trattata a questo link oppure qui (in lingua inglese). E' importante la distinzione fra ramo ascendente e discendente.

Figura 1. Un esempio di idrogramma (da Wikipedia)

La stima dell'idrogramma completo è necessaria nella progettazione di casse di espansione, dighe ed altre strutture che debbono essere dimensionate sulla base della conoscenza del volume idrico associato ad un evento di piena. Altre strutture quali gli argini sono in molti casi pratici progettate sulla base della conoscenza della sola portata al colmo, così come le briglie ed altre strutture minori. Nella prima parte di questa lezione ci concentreremo sulla stima della portata di piena.

La portata e l'ìdrogramma di piena si riferiscono ad un assegnato tempo di ritorno ed un'assegnata sezione fluviale trasversale, la quale a sua volta è riferita al bacino contribuente.

La stima della portata di piena, così come la stima di ogni variabile di progetto, richiede la specifica di dettagli progettuali, ed in particolare del tempo di ritorno, il quale essenzialmente definisce quanto la portata di piena è "estrema".

In statistica ed ingegneria si quantifica l'eccezionalità di un evento specificandone la frequenza di accadimento. In particolare, in ingegneria si quantifica la frequenza di accadimento di un evento specificandone il tempo di ritorno. Facendo riferimento alla portata di piena, il tempo di ritorno è il tempo medio che intercorre fra due eventi la cui portata al colmo è uguale o superiore ad un valore assegnato. E' possibile quindi affermare che "il tempo di ritorno della portata fluviale pari a 13.000 m³/s per il Fiume Po a Pontelagoscuro è circa 100 anni".

La stima del tempo di ritorno sarebbe relativamente semplice se si disponesse di lunghe serie di portata fluviale osservata. Ad esempio, se fossero disponibili osservazioni di portata fluviale per 100 anni, si potrebbe affermare che il valore più elevato ha tempo di ritorno di circa 100 anni. La stima è comunque approssimativa poichè un numero finito di osservazioni, ancorchè alto, non è pienamente rappresentativo delle caratteristiche intrinseche del fenomento in studio. L'approssimazione diviene evidente considerando che le osservazioni ipoteticamente raccolte nei 100 anni successivi porgerebbero una stima diversa, poichè ovviamente il fenomeno non si ripeterebbe con le medesime modalità.

E' importante perciò distinguere la struttura fisica del fenomeno, che generalmente è regolato da leggi fisiche assegnate, dalla "realizzazione" del fenomeno stesso, ovvero ciò che noi osserviamo. Considerando quindi una ipotetica serie temporale di estensione centenaria, potremmo dire che il secondo valore, a partire dal più alto, ha un tempo di ritorno di circa 50 anni, a condizione che sia indipendente dal valore più alto, ovvero si sia verificato durante un evento indipendente. Il terzo valore avrebbe un tempo di ritorno pari a circa 33 anni e così via. Procedendo con questo calcolo ci si renderebbe facilmente conto che il valore medio ha un tempo di ritorno di circa 2 anni.

Il tempo di ritorno dipende quindi dal valore della portata fluviale, ed in particolare aumenta all'aumentare della portata stessa. Possiamo quindi concludere che progettare una struttura per tempo di ritorno elevato significa ottenere un sovradimensionamento, e quindi una soluzione più onerosa dal punto di vista economico, rispetto ad assumere tempi di ritorno inferiori. Il tempo di ritorno rispetto al quale una struttura deve essere progettata è solitamente prescritto da normative. Ad esempio, la Direttiva Europea "Flood Directive" prescrive agli Stati membri l'individuazione di aree allagabili a rischio medio, assumendo quale tempo di ritorno di progetto un valore pari ad almeno 100 anni.

I modelli di stima della portata di piena sono solitamente divisi in due grandi categorie: modelli probabilistici e modelli deterministici.

I modelli probabilistici si basano sulla inferenza statistica la quale a sua volta si basa sull'analisi della frequenza di accadimento dei picchi di piena nei dati osservati. I modelli probabilistici possono anche recare una stima dell'incertezza associata alla variabile di progetto, che è un'informazione essenziale per la progettazione.

I modelli deterministici invece si basano sull'applicazione di una relazione matematica che porge il valore stimato della variabile di progetto senza recare alcuna informazione sull'incertezza. Alcuni metodi di stima della portata di piena di progetto si basano sull'uso di modelli afflussi-deflussi, ovvero modelli matematici che ricostruiscono le portate fluviali in funzione di assegnate variabili in ingresso, fra le quali sempre compare la precipitazione.

I modelli afflussi-deflussi sono tipicamente utilizzati quando non sono disponibili dati osservati di portata fluviale. In questi casi l'idea è quella di ricostruire i deflussi fluviali in funzione delle precipitazioni osservate, che sono di solito più facilmente disponibili. Tuttavia la classificazione in modelli probabilistici e deterministici è oggi obsoleta. Infatti, classificando i modelli di stima della portata di piena in categorie si induce l'inappropriata sensazione che il deflusso fluviale, ovvero il processo fisico che noi osserviamo, possa essere originato da diversi fenomeni fisici. In realtà il fenomeno è uno solo, ed i modelli porgono solo un'interpretazione. I modelli dovrebbero quindi avere una radice comune, ovvero la base fisica, e dovrebbero differenziarsi solo per i metodi applicati per utilizzare l'informazione disponibile, od al limite per l'interpretazione che essi adottano di fenomeno ancora non del tutto noti.

Il deflusso fluviale di piena è generato da un fenomeno fisico che evolve in ambiente fortemente affetto da impatto antropico. Le forzanti del fenomeno non sono quindi solo naturali, ma in molti casi anche antropogeniche. Si conosce ancora poco di detto fenomeno fisico e non saremo mai in grado di conoscerlo compiutamente e quindi di interpretarlo senza incertezza. Poichè quindi il fenomeno è unico, è opportuno definire un unico modello di stima. In considerazione dell'incertezza che sempre è associata al responso del modello di stima, sarebbe a rigore inappropriato applicare un modello deterministico. Parte dell'incertezza è dovuta all'impossibilità di descrivere nel dettaglio la geometria del sistema (volume di controllo) e parte è dovuta alla nostra conoscenza ancora limitata dei fenomeni. La presenza di incertezza implica che il modello appropriato per stimare la portata di piena è un modello probabilistico (stocastico) e quindi la conclusione è che una unica classe di modelli dovrebbe essere utilizzata, ovvero i modelli probabilistici.

Tuttavia, poichè il modello di stima in oggetto descrive un processo fisico, ovvero un processo che è essenzialmente governato dalle leggi della fisica, il modello probabilistico dovrebbe essere sempre supportato da una base fisica, in accordo al principio che tutta l'informazione disponibile dovrebbe essere utilizzata per supportare la stima, al fine di ridurre l'incertezza. In conclusione, se ne deduce che il modello di stima della portata di piena dovrebbe essere di natura probabilistica e fisicamente basata.

Cosa esattamente significa "modello fisicamente basato"? Si consideri, innanzitutto, che i modelli idrologici sono essenzialmente finalizzati ad interpretare processi di deflusso di liquidi; ovvero, processi di trasferimento di massa che implicano pure il trasferimento e trasformazioni di energia. Si tratta di processi che sono governati dalla meccanica dei fluidi, per i quali valgono i principi di conservazione della massa, conservazione dell'energia e conservazione della quantità di moto.

In meccanica dei fluidi sono altresì verificate le leggi di Newton. Queste vennero derivate nel 1687 da Isaac Newton. Possiamo quindi concludere che un modello matematico di processi idrologici dovrebbe essere basato sull'applicazione dei suddetti principi di conservazione, pur tenendo presente che altri principi, oltre quelli della fisica, possono essere applicati nell'ambito delle scienze idrologiche. Ad esempio, possono essere applicati principi fondamentali di ecologia, chimica e scienze sociali.

E' importante considerare che l'incertezza innanzi menzionata è una caratteristica del modello di stima che utilizziamo per descrivere il processo fisico (oppure ecologico, chimico etc.) in oggetto. L'incertezza non è una caratteristica del fenomeno. Quest'ultimo dà luogo ad una unica traiettoria. Sarebbe dunque inappropriato affermare che il fenomeno è stocastico oppure deterministico. Termini quali "deterministico", "probabilistico" e "incertezza" si riferiscono al modello che utilizziamo per descrivere il processo fisico, il quale è basato su assunzioni. La validità di queste assunzioni dovrebbe sempre essere verificata, mediante analisi basata su intuizione oppure considerazioni fisicamente basate.

I modelli stocastici fisicamente basati assumono che le piene fluviali possano essere descritte quali eventi casuali, ovvero, eventi che non possono essere descritti mediante un modello deterministico. Gli eventi casuali non possono essere previsti con esattezza, tuttavia in molti casi sono caratterizzati da regolarità. Queste ultime sono determinate da una causa, che nel nostro caso è originata dalle leggi della fisica. Non sempre, tuttavia, è possibile determinare analiticamente la natura della causalità che viene osservata in un evento casuale.

Figura 2. Il lancio dei dadi è un classico esempio di evento casuale (da Wikipedia)

Per trattare eventi casuali e per trarre deduzioni dalla loro osservazione, è necessario associare a detti eventi un valore numerico. Questa associazione dà luogo alla variabile casuale, la quale è definita quale associazione fra un evento casuale e un numero reale (oppure intero o complesso). Nel nostro caso, noi trattiamo la portata di piena quale variabile casuale, ovvero un'associazione tra un evento di piena ed un numero reale.

Le variabili casuali possono essere discrete o continue. Nel primo caso il numero delle possibili realizzazioni è finito, mentre nel secondo caso è infinito.

Il modello stocastico fisicamente basato è quindi chiamato a produrre una stima di portata al colmo intesa quale variabile casuale, utilizzando un approccio fisicamente basato. In questo modo abbiamo anche la possibilità di tenere conto dell'impatto antropico.

Per comprendere l'essenza e le possibili strutture di un modello stocastico fisicamente basato abbiamo necessità di introdurre alcuni (pochi) concetti di base di teoria della probabilità.

1.2.1. Fondamenti di teoria della probabilità

La probabilità descrive null'altro che la frequenza con la quale un evento viene osservato. La probabilità è quantificata mediante un numero variabile fra 0 e 1, ove 0 indica impossibilità ed 1 indica certezza. Maggiore è la probabilità di un evento e maggiore sarà la frequenza con la quale viene osservato. La probabilità può essere definita mediante gli assiomi di Kolmogorov, che devono essere soddisfatti comunque la probabilità sia definita. Detti assiomi possono essere enunciati come segue:

• La probabilità di un evento è un numero reale non negativo;
• La probabilità dell'intero spazio campione è 1;
• La probabilita' dell'unione di due eventi mutuamente esclusivi è data dalla somma delle loro singole probabilità.

Partendo dal presupposto che la probabilità può essere stimata mediante un'analisi oggettiva di un esperimento oppure attraverso l'intuizione, ovvero attraverso due diversi tipi di indagine, si perviene a due definizioni diverse di probabilità. La definizione frequentista definisce la probabilità di un evento quale il limite della sua frequenza relativa in un numero molto ampio di esperimenti. Si noti che tale definizione soddisfa gli assiomi di Kolmogorov. La definizione Bayesiana associa invece la probabilità a una quantità che sintetizza una conoscenza, oppure una intuizione. Questa definizione può pure soddisfare gli assiomi di Kolmogorov, avendo cura di porre dei vincoli alla stima.

La definizione frequentista e quella Bayesiana non sono in contrapposizione. L'approccio frequentista è utilizzato quando sia possibile effettuare esperimenti ripetuti (ad esempio nel caso classico del lancio dei dadi oppure di una moneta), mentre il metodo Bayesiano è particolarmente vantaggioso quando non è possibile effettuare un esperimento, oppure questo è possibile solo per un numero limitato di tentativi. L'approccio Bayesiano presenta il vantaggio di poter incorporare conoscenze a priori, ad esempio derivate dalla conoscenza della fisica del fenomeno.

1.2.2. Distribuzione di probabilità

La distribuzione di probabilità è una relazione analitica che permette di attribuire una probabilità ad un assegnato evento casuale. Chiaramente la distribuzione di probabilità deve necessariamente essere messa a punto analizzando osservazioni. Per definire una distribuzione di probabilità è necessario distinguere fra variabile casuale continua e discreta.

Nel caso discreto è possibile stimare la probabilità semplicemente facendo esperimenti multipli oppure mediante intuizione. Ad esempio, nel caso del lancio dei dadi si intuisce facilmente, e detta intuizione potrebbe essere velocemente verificata mediante prove sperimentali, che ognuno dei 6 possibili risultati ha probabilità pari a 1/6.

Nel caso di una variabile casuale reale, quale ad esempio il deflusso fluviale, si intuisce facilmente che il numero dei possibili risultati è infinito e quindi la probabilità di ciascuno di essi tende al valore nullo. Occorre quindi riferirsi ad intervalli dei valori assumibili dalla variabile onde limitare il numero dei possibili risultati. Così facendo, si perviene alla definizione di densità di probabilità.

Supponiamo che un intervallo di lunghezza 2Δx sia centrato attorno ad un valore generico e reale x della variabile casuale X, dagli estremi dell'intervallo x-Δx e x+Δx. Se vengono ripetuti esperimenti di realizzazione di X (se X rappresenta una portata di piena l'esperimento consiste semplicemente nell'estrazione di un valore dalla serie storica), la frequenza degli eventi che ricadono all'interno dell'intervallo innanzi definito può essere stimata con la relazione: F_r(x-Δx;x+Δx) = N(x)/N, dove N(x) è il numero di risultati dell'esperimento che ricadono nell'intervallo e N è il numero totale degli esperimenti.

Possiamo ora definite la densità di probabilità di x, f(x), come:

Se esiste una funzione analitica per la f(x), questa è la funzione di densità di probabilità, oppure distribuzione di densità di probabilità, ed è indicata anche con il simbolo "pdf". Se la densità di probabilità è integrata sull'intervallo di definizione di X, dal suo estremo inferiore fino al valore considerato x, si ottiene la probabilità che la variabile casuale sia non più grande di x, ovvero si ottiene la probabilità di non superamento. L'integrale della densità di probabilità può essere calcolato per qualunque valore di X ed è indicato con il termine "probabilità cumulata". Integrando la f(x), qualora l'integrale stesso esista, si ottiene la funzione di probabilità cumulata F(X), che è spesso indicata con il simbolo "CDF".

Figura 3. La probabilità p(S) porge la distribuzione della probabilità della somma S del risultato complessivo del lancio di due dadi. Ad esempio, la figura mostra che p(11) = 1/18. La conoscenza della probabilità dei singoli eventi consente la stima di probabilità cumulata di eventi quali P(S > 9) = 1/12 + 1/18 + 1/36 = 1/6.

Esempio: La distribuzione Gaussiana o normale La distribuzione Gaussiana o normale, sebbene non sia molto utilizzata per rappresentare variabili idrologiche, è un esempio molto interessante di distribuzione di densità di probabilità. Dalla pagina di Wikipedia in inglese che descrive la distribuzione Gaussiana si traduce: "In teoria della probabilità, la distribuzione normale (o Gaussiana) è spesso utilizzata nelle scienze naturali o sociale per descrivere variabili casuali reali [...]. La distribuzione normale ha una interessante proprietà che è sintetizzata dal teorema del limite centrale. Questo, nella sua forma più generale e sotto opportune condizioni, fra le quali quella che la variabile casuale considerata abbia varianza finita, afferma che la media di variabili casuali che siano indipendentemente estratte da funzioni di probabilità indipendenti converge in distribuzione alla Gaussiana per numero delle variabili casuali tendente ad infinito. Grandezze fisiche che risultatano dalla somma di numerosi processi indipendenti, quali ad esempio gli errori di misura, spesso sono caratterizzate da distribuzioni che sono approssimativamente normali". La distribuzione di densità di probabilità Gaussiana si scrive nella forma (da Wikipedia):

dove μ è la media della distribuzione e σ è la deviazione standard.

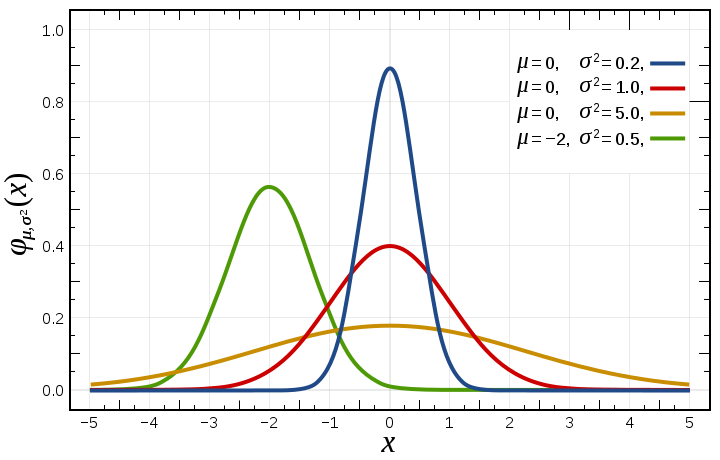
Figura 4. Funzione di densità di probabilità della distribuzione Gaussiana (da Wikipedia)

L'introduzione innanzi presentata alla teoria della probabilità porge quale logica conseguenza un metodo ampiamente utilizzato per la stima delle portate al colmo, che si avvale di distribuzioni di probabilità per descrive la frequenza di accadimento degli eventi di piena. Abbiamo infatti già messo in evidenza come il tempo di ritorno, che è un'informazione essenziale per la stima della portata fluviale di piena, possa essere direttamente collegato a detta frequenza di accadimento e quindi alla probabilità di non superamento, la quale può essere stimata applicando una opportuna distribuzione di probabilità. Questo metodo può essere interpretato nel contesto della teoria degli approcci stocastici fisicamente basati.

Infatti, il tempo di ritorno può essere interpretato quale l'inverso del numero atteso degli eventi nel tempo pari al passo temporale di osservazione. Ad esempio, il valore della portata fluviale massima annuale con tempo di ritorno pari a 10 anni, sotto assunzioni non vincolanti dal punto di vista tecnico, è caratterizzato da una probabilità pari a 1/10=0.1, quindi il 10%, di essere superato in un anno; il valore con tempo di ritorno pari a 50 anni è associato ad una probabilità del 2% e così via. Quindi, fissato il tempo di ritorno è possibile stimare il valore della variabile casuale associata invertendo la distribuzione di probabilità che ne regola la frequenza di accadimento.

La stessa distribuzione di probabilità può essere utilizzata per valutare l'incertezza della stima. In idrologia applicata la distribuzione di probabilità delle portate al colmo è solitamente stimata valutando la frequenza di accadimento dei valori di portata massima annuale (si veda, ad esempio, quanto descritto qui (in lingua inglese)). Il metodo si applica estraendo innanzitutto i valori di portata al colmo massima annuale dai dati osservati, che vengono successivamente utilizzati per stimare i parametri di una assegnata distribuzione di probabilità. Il tempo di ritorno dei valori di portata massima annuale può essere definito, in questo caso, quale numero medio di anni che intercorre fra due valori di portata massima annuale uguali o superiori ad una soglia assegnata.

Il metodo dei massimi annuali è condizionato dall'assunzione che il processo stocastico che governa la formazione dei deflussi massimi annuali sia indipendente e stazionario. Si tratta delle assunzioni poco vincolanti dal punto di vista tecnico innanzi menzionate.

L'indipendenza implica che gli eventi che generano la portata massima annuale siano generati da processi meteorologici ed idrologici diversi e mutualmente non influenzati. Quest'assunzione è generalmente soddisfatta in pratica poichè questi eventi sono generalmente ben lontani fra loro nel tempo. Tuttavia, occorre verificare che la stagione delle piene non interessi i medi di dicembre e gennaio, circostanza che potrebbe originare eventi contigui nel tempo in anni diversi; inoltre, è necessario tenere presente che si possono verificare fenomeni di memoria a lungo termine che potrebbero implicare la presenza di dipendenza particolarmente protratta nel tempo.

L'assunzione di stazionarietà è oggetto di vivaci discussioni in ambito scientifico poichè variazioni delle condizioni ambientali, ed in particolare cambiamenti climatici, potrebbe renderla non attendibile. Alcune recenti pubblicazioni scientifiche pongono in discussione il concetto stesso di tempo di ritorno in presenza di cambiamenti significativi nella dinamica dei processi stocastici interessati dalla formazione delle piene fluviali. Tuttavia, l'assunzione di stazionarietà rimane spesso conveniente in ambito tecnico al fine di poter estrarre utili informazioni dai dati osservati. Ulteriori informazioni sul dibattito scientifico in merito all'assunzione di stazionarietà possono essere trovate qui (in lingua inglese) e qui (in lingua inglese).

La probabilità associata ai deflussi massimi annuali può essere stimata utilizzando diverse formulazioni per la relativa funzione di distribuzione. L'approccio più utilizzato in ambito tecnico si basa sull'utilizzo della Distribuzione di Gumbel, che si scrive nella forma:

F(x) = e^-e-(x-μ)/β

dove μ e β sono parametri. La mediana, ovvero il valore di portata fluviale che corrisponde al massimo della densità di probabilità, si calcola mediante la relazione

mentre la media della distribuzione è pari a

dove è la costante di Eulero–Mascheroni, Lo scarto quadratico medio della distribuzione si ottiene dalla relazione

σ = .

Da quanto sopra derivano le relazioni per la stima dei parametri della distribuzione che seguono, che sono quelle applicate dal punto di vista tecnico: β=σ/1.283, μ=m-0.45 σ dove σ e m sono, rispettivamente, lo scarto quadratico medio e la media del campione di osservazioni disponibili. Quindi, una volta che sia a disposizione un campione di lunghezza sufficiente di osservazioni di portata massima annuale, i parametri della distribuzione di Gumbel sono facilmente stimabili. La distribuzione di Gumbel è stata proposta da Emil Julius Gumbel nel 1958.

Esempio di applicazione - Il metodo dei massimi annuali e la distribuzione di Gumbel

Si supponga che siano disponibili le seguenti 10 osservazioni di portata massima annuale, espresse in m³/s, per la stima della portata al colmo con tempo di ritorno pari a 5 anni:

239.0; 271.1; 370.0; 486.0; 384.0; 408.0; 148.0; 335.0; 315.0; 508.0

La media delle osservazioni è pari a 346.41 m³/s e lo scarto quadratico medio è pari a 110.08 m³/s. Si ottiene quindi che β=85.80 and μ=296.88. La probabilità di non superamento corrispondente al tempo di ritorno di 5 anni è P(Q)=(T-1)/T=4/5=0.8. Invertendo la distribuzione di Gumbel si ottiene:

Q(T)= -β(log(-log(P(Q))))+μ

oppure

Q(T)= -β(log(log(T/(T-1))))+μ

Si ottiene: Q(5)=383.8 m³/s

1.3.1. Verifica della bontà della stima

Nel momento in cui si applica una distribuzione di probabilità per descrivere la frequenza di accadimento di eventi estremi è necessario chiedersi se la distribuzione prescelta sia attendibile. Per verificare la bontà della stima si può applicare un test statistico. Il più utilizzato per verificare distribuzioni di probabilità è il test di Kolmogorov–Smirnov, il quale confronta la probabilità di non superamento di ciascun dato, fornito dalla distribuzione di Gumbel, con la frequenza di non superamento empirica calcolata sui dati. Il test si articola nei passi che seguono:

1. Si ordinano i dati di portata massima annuale in ordine crescente e si associa ad ogni dato un numero d'ordine i. Il dato più piccolo sarà associato a i=1 ed il più grande a i=N dove N è il numero totale di osservazioni.
2. Per ogni dato, si calcola la frequenza di non superamento F*= i/(N+1); il denominatore si assume pari a N+1 per non associare al dato più grande probabilità di non superameno uguale ad 1, il che non sarebbe fisicamente sensato (dividendo per N+1 si applica la "Weibull plotting position").
3. Per ogni dato, si calcola la probabilità di non superamento P data dalla distribuzione di Gumbel.
4. Si calcola il valore assoluto della massima differenza fra F e P, ovvero \(\epsilon=\max_{i=1}^{N}|F_i-P_i|\).
5. Si verifica che \(\epsilon\leq K\) dove K è il valore massimo accettabile.

Per livello di confidenza pari al 95% \(K=\frac{1.36}{\sqrt(N)}\).

Si veda la Figura 7. Per una descrizione di maggiore dettaglio si prega di leggere qui.

Figura 7. Il test di Kolmogorov–Smirnov. Nella figura, X è una generica variabile casuale che può assumere valori sia positivi sia negativi. La linea rossa è la CDF, la linea blu è la distribuzione di frequenza calcolata sul campione, e la la freccia nera indica la statistica di Kolmogorov-Smirnon (da Wikipedia).

1.3.2. Dati richiesti per l'applicazione del metodo dei massimi annuali

Il metodo dei massimi annuali richiede quindi la disponibilità di serie sufficientemente lunghe di dati di deflussi massimi annuali. All'aumentare del tempo di ritorno della stima aumenta l'incertezza della stima stessa ed è quindi bene che aumenti pure la dimensione del campione di dati. Una regola empirica suggerisce di non estrapolare la distribuzione di Gumbel oltre tempi di ritorno doppi rispetto alla dimensione del campione di dati, ma è bene cercare di mantenersi al di sotto di tale limite. La distribuzione di Gumbel tende a sovrastimare la variabile di progetto se utilizzata in estrapolazione, ma è comunque bene evitare in ogni caso incertezze eccessive.

La raccolta dei dati è spesso un problema rilevante per il progettista. In Italia vi sono numerosi enti che raccolgono dati, ma non sempre questi vengono resi disponibili e non sempre è chiaro a quale ente occorre rivolgersi. Oggi in Italia il riferimento principale per i dati idrologici è l'ex Servizio Idrografico e Mareografico nazionale, ora assorbito dalle Agenzie Regionali per la Protezione dell'Ambiente (ARPA). Fino a circa 20 anni or sono l'ufficio curava la pubblicazione degli Annali Idrologici, che raccoglievano e sistematizzavano l'informazione disponibile. Un esempio di annale può essere scaricato qui.

1.3.3. Le basi fisiche del metodo dei massimi annuali

Il metodo dei massimi annuali è un approccio essenzialmente probabilistico, ma nella realtà può essere considerato un metodo stocastico fisicamente basato, ove l'informazione di natura fisica è recata dai dati. Infatti, il campione di osservazioni di deflusso massimo annuale porta con se una notevole informazione a proposito dei processi fisici che regolano la formazione delle precipitazioni. Tuttavia, è chiaro che la base fisica del metodo dei massimi annuali è limitata. E' quindi interessante chiedersi come potrebbe essere possibile incorporare nel metodo dei massimi annuali una maggiore informazione fisicamente basata, che consentirebbe di ridurre l'incertezza della stima e consentirebbe anche di stimare l'effetto dell'impatto antropico.

A questo scopo, è necessario investigare con maggiore dettaglio come l'informazione recata dai dati è utilizzata nell'analisi statistica. Il contenuto d'informazione è estratta dai dati, applicando il metodo dei massimi annuali, attraverso la stima del valore medio E(X) e lo scarto quadratico medio σ(X) della variabile casuale X, ovvero il deflusso massimo annuale. Sono queste e solo queste le statistiche che vengono utilizzate per calibrare la distribuzione di Gumbel e derivare la variabile di progetto.

Ci si dovrebbe quindi chiedere come potrebbe essere possibile supportare la stima di E(X) e σ(X) con maggiore informazione. Ad esempio, si potrebbe utilizzare informazione derivata dalla conoscenza delle caratteristiche del bacino contribuente, oppure l'informazione recata da altri metodi di stima, quali ad esempio i modelli afflussi-deflussi. Sulla base di queste informazioni addizionali potrebbe essere affinata la stima di E(X) e σ(X). Una stima ulteriore di E(X) potrebbe essere fornita da relazioni regionali, come più sotto chiarito.

1.3.4. Distribuzioni di probabilità alternative per il metodo dei massimi annuali

Vi sono numerose distribuzioni di probabilità che possono essere utilizzate per il metodo dei massimi annuali in alternativa alla distribuzione di Gumbel, ad esempio Distribuzione di Frechet e la Distribuzione GEV, la quale include la Distribuzione di Gumbel e quella di Frechet quali casi particolari.

1.3.5. Il metodo delle eccedenze (POT)

Il metodo dei massimi annuali presenta lo svantaggio di utilizzare, per l'inferenza statistica, un solo valore di portata al colmo per anno. Sussiste quindi il rischio che i dati relativi a piene potenzialmente significative non siano utilizzati sono perchè la portata al colmo è risltata inferiore al massimo di quell'anno. Questo problema è superato dall'applicazione del metodo delle eccedenze (POT), il quale analizza tutti i colmi di piena che hanno superato un valore di soglia limite prefissato. Le distribuzioni di probabilità che sono prese in considerazione dal metodo delle eccedenze sono diverse rispetto al metodo dei massimi annuali. Maggiori dettagli sono forniti qui.

In molte applicazioni tecniche risulta difficile rinvenire dati di deflussi fluviali osservati alla sezione di interesse, oppure è possibile rinvenire dati solo in misura limitata, e quindi il metodo dei massimi annuali non può essere applicato. In tali situazioni è necessario applicare metodi di stima per bacini fluviali non strumentati, o scarsamente strumentati. Tali metodi si propongono di utilizzare informazioni di natura diversa rispetto ai dati, che possono riferirsi al corso d’acqua considerato, al relativo bacino imbrifero ed alla climatologia della zona.

Un metodo che è frequentemente applicato in ambito tecnico è quello di riferirsi a dati di deflusso fluviale osservati in località limitrofe, per le quali si perviene alla stima della portata al colmo di piena che viene successivamente ragguagliata alla sezione di interesse utilizzando criteri di similarità. Ad esempio, si può assumere che il deflusso fluviale di piena incognito Q(T) corrispondente al tempo di ritorno T sia dato dalla relazione:

dove Q_* è la portata al colmo nella sezione strumentata di riferimento, ed A e A_* sono le aree dei bacini contribuenti per le sezioni non strumentata e strumentata, rispettivamente, e α è un esponente per il quale la letteratura suggerisce il valore di1/3, il quale significa che il contributo specifico alla portata di piena (cioè, il contributo di piena per unità di area contribuente) è crescente al calare dell’estensione del bacino imbrifero.

1.4.1. Il metodo della piena indice

Il concetto di similitudine idrologica può essere esteso riferendosi ad un insieme esteso di sezioni fluviali di riferimento, piuttosto che ad una singola località. L’insieme viene identificato raggruppando tutte le sezioni fluviali incluse all’interno di una cosiddetta “regione omogenea”. Per tutte le sezioni così identificate si assume che la portata al colmo Q(x,T) nella sezione x, corrispondente al tempo di ritorno T, possa essere espressa mediante la relazione:

Q(x,T) = i(x) F(T),

dove i(x) è la media dei deflussi massimi annuali nella sezione fluviale di interesse ed è detta "piena indice" e F(T) è la cosiddetta “curva di fequenza regionale”, che è assunta essere invariante nella regione omogenea.

La curva di frequenza regionale è stimata mediante una opportuna distribuzione di probabilità, la quale è parametrizzata utilizzando tutti i dati disponibili di portata fluviale adimensionale al colmo (cioè portata al colmo divisa per la piena indice) per la regione omogenea. Questo approccio presenta il vantaggio di permettere di allargare il campione dei dati disponibili, che ora include tutte le osservazioni note per la regione omogenea, rispetto alla stima effettuata su una sola sezione fluviale. Rimane da effettuare, per la sezione fluviale di riferimento, la stima della piena indice, che può essere ottenuta calcolando la media dei deflussi massimi annuali con un metodo opportuno che possa sfruttare convenientemente l’informazione disponibile. Se sono disponibili osservazioni, anche in numero limitato, di portata massima annuale, una soluzione possibile è calcolarne semplicemente il valore medio, con il vantaggio che l’incertezza associata alla stima della media è molto minore rispetto alla stima diretta della portata al colmo. Infatti, esperienze presentate dalla letteratura hanno dimostrato che la piena indice può essere stimata con approssimazione soddisfacente calcolando il valore medio di anche solo 5 osservazioni. In assenza di dati osservati, la piena indice può essere calcolata mediante relazioni di regressione, ove le variabili indipendenti possono essere assegnate caratteristiche morfologiche, geologiche e climatiche del bacino imbrifero.

La portata al colmo è solitamente stimata estraendo i valori massimi da una serie temporale di deflussi medi nel corso del passo temporale di osservazione. Ad esempio, spesso i deflussi fluviali sono osservati a scala temporale giornaliera, raccogliendo l’osservazione a orario fissato nel corso della giornata. Le osservazioni che ne risultano vengono assunte essere rappresentative del valore medio di portata nel corso del giorno, dai quali vengono poi estratti i valori massimi annuali (od i valori eccedenti un’assegnata soglia).

Tuttavia, è evidente che il deflusso massimo giornaliero non è coincidente con il deflusso osservato ad un assegnato istante durante il giorno, che è generalmente inferiore rispetto alla portata al colmo. L’entità della differenza dipende dalla dimensione del bacino, il tempo di corrivazione, la stagione, il clima e così via. Di particolare importanza è il ruolo del tempo di corrivazione, ovvero il tempo che occorre alla generica goccia di pioggia caduta nel punto idraulicamente più lontano a raggiungere la sezione di chiusura del bacino in esame. A parità di altre condizioni, un tempo di corrivazione più esteso corrisponde a minore entità della portata di piena. La letteratura ha proposto diverse relazioni di tipo empirico per la stima del rapporto fra il massimo del deflusso giornaliero ed il deflusso massimo annuale. Le più utilizzate sono le Formule di Cotecchia. Per maggiori dettagli si veda, ad esempio, questa dispensa del prof. Moisello (Università di Pavia).

E’ stato in precedenza menzionato che il processo di formazione delle portate fluvial al colmo è essenzialmente di natura fisica, ovvero un processo che è regolato dalle leggi di Newton e dalle leggi di conservazione della massa e dell’energia. Queste leggi di natura fisica non sono direttamente utilizzate dal metodo dei massimi annuali e dagli altri metodi in precedenza trattati. Nelle applicazioni tecniche possono essere applicati metodi di stima che si basano sulla applicazione diretta delle leggi della fisica, soluzione che può essere utile in completa assenza di dati di deflusso osservati. Questi metodi si traducono nella messa a punto di un modello afflussi-deflussi, che descrive la trasformazione pioggia-portata applicando le leggi fisiche innanzi menzionate.

Un modello afflussi-deflussi porge la stima della portata al colmo di piena in dipendenza da una o più variabili in ingresso. E’ necessaria almeno una variabile in ingresso, ovvero la precipitazione, ma possono essere incluse altre variabili quali la temperatura, la velocità del vento, la morfologia del bacino contribuente e così via. Il modello può porgere la stima della sola portata al colmo oppure dell’intero idrogramma. Allo stesso modo, le variabili in ingresso possono essere costituite da valori puntuali o da serie temporali. Nel seguito verranno descritte le soluzioni più utilizzate, soffermandosi sui loro fondamenti fisici e la loro incertezza.

1.6.1. La formula razionale

La formula razionale porge una stima della portata fluviale al colmo Q [L³/T] per un bacino idrografico di area A [L²], in dipendenza di una forzante di precipitazione di intensità i [L/T] ed in dipendenza di un coefficiene chiamato “coefficiente di deflusso” C [-]. La formula razionale può essere considerato il primo esempio di modello afflussi-deflussi; fu proposta dall’americano Kuichling in 1889, che elaborò concetti in precedenza proposti dall’ingegnere irlandese Thomas Mulvaney nel 1851.

La formula razionale si scrive nella forma:

Q = C i A,

è dimensionalmente omogenea e quindi la precipitazione deve essere espressa in m/s e l’area del bacino in m², per ottenere una stima del deflusso fluviale in m³/s. La stima dell’intensità di pioggia i da utilizzare nella formula razionale richiede una considerazione approfondita. E’ intuitivo che si debba utilizzare un’intensità di precipitazione estrema, la quale deve essere espressa in funzione del tempo di ritorno rispetto al quale si intende stimare la portata al colmo. Inoltre, è intuitivo che l’intensità di precipitazione deve dipendere dalla durata dell’evento di pioggia, poiché è noto che ad eventi di durata decrescente corrispondono intensità di precipitazione crescenti.

L’intensità di precipitazione è solitamente stimata mediante la curva di possibilità pluviometrica, o curva di possibilità climatica, in funzione del tempo di ritorno. Nell’applicazione della Formula Razionale si assume frequentemente che il tempo di ritorno della portata al colmo sia coincidente con il tempo di ritorno della precipitazione che l’ha indotta. Si tratta di un’assunzione non verificata in pratica, ma che rappresenta comunque una valida ipotesi di lavoro. Le ulteriori assunzioni della formula razionale sono elencate nel seguito.

In merito alla durata dell’evento di precipitazione, può essere dimostrato, introducendo opportune ipotesi semplificative, che la durata di pioggia che causa la situazione più critica in termini di portata al colmo è pari al tempo di corrivazione del bacino contribuente. E’ importante inoltre osservare che il valore medio areale della precipitazione, piuttosto che un valore puntuale, dovrebbe essere utilizzato nella formula razionale. Per bacini di estensione significativa, (più di 10 km²) si dovrebbe stimare i facendo riferimento ai dati raccolti da un pluviometro collocato in posizione centrale rispetto all’estensione dell’area contribuente e successivamente dovrebbe essere applicato un fattore di riduzione all’area. Per ulteriori dettagli si vedano le dispense del Politecnico di Torino disponibili qui.

Il tempo di corrivazione è definito come il tempo necessario per la particella fluida che cade nella posizione idraulicamente più remota del bacino a raggiungere la sezione di chiusura. Chiaramente questo tempo non è misurabile, ed è solitamente stimabile con relazioni empiriche. Nel contesto italiano è solitamente utilizzata la formula di Giandotti.

Una complicazione rilevante nell’applicazione della formula razionale è la stima del coefficiente di deflusso, che generalmente varia da 0.4 a 0.6 nei bacini idrografici non eccessivamente impattati da attività di origine antropica.

Singh (1992, p. 598) discute le assunzioni che condizionano la validità della formula razionale. Le più rilevanti sono:

1. “Il tempo di ritorno di precipitazione e portata fluviale coincidono" (vedi sopra).

2. “Il coefficiente di deflusso è costante al variare del tempo di ritorno, il che significa che le perdite idriche non variano al variare del tempo di ritorno."

3. “Il coefficiente di deflusso è costante al variare dell’intensità di pioggia e non è quindi dipendente dall’umidità antecedente."

4. “La pioggia è distribuita uniformemente nel tempo per tutta la durata dell'evento."

5. “La pioggia è distribuita uniformemente sul bacino idrografico."

Nonostante sia molto semplice ed affetta da considerevoli approssimazioni, la formula razionale è estremamente utile in idrologia per aumentare la base fisica a supporto della stima e per ottenere una prima stima da utilizzarsi per un confronto.

Ultima modifica effettuata il giorno 22 novembre 2022